ABSTRACT
We present a system for generation and recognition of oscillatory gestures. Inspired by gestures used in two representative human-to-human control areas, we consider a set of oscillatory (circular) motions and refine from them a 24 gestures lexicon. Each gesture is modeled as a dynamic system with added geometric constraints to allow for real time gesture recognition using a small amount of processing time and memory. The gestures are used to control a pan-tilt camera neck. We propose extensions for use in areas such as mobile robot control and telerobotics.
Developing A Gesture Lexicon
Sociological and biological research on human created gestures suggests that while gestures have standard meanings within a society, no known body motion or gesture has the same meaning in all societies [1]. Even in American Sign Language, few signs are so clearly transparent that a non-signer can guess their meaning without additional clues [6]. Thus we are free to create gestures for device control as we see fit.
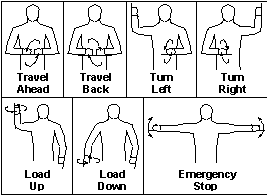
Examples of a Human Gesture Control Environment.
Two areas in which gesture languages have developed to communicate commands are crane and excavator and runway traffic control. A sample set of crane control gestures, shown in Figure 1 [3], is composed of oscillating planar motions, that is, circles or back-and-forth lines made in two dimensions in real world three dimensional space. Certain gestures used to signal aircraft on a runway are also planar oscillators [10].
The use of gestures in these environments shows that oscillatory motions are useful for several reasons. First, oscillatory motions are recognizable by other humans and used in critical and potentially dangerous areas. Second, humans can easily and consistently make oscillatory motions. Third, some oscillatory gestures have time dependent content which can be created and understood by humans. For example, the "travel ahead" gesture's circular velocity is increased when a faster response is desired.
An "Oscillating Motion" Gesture Lexicon.
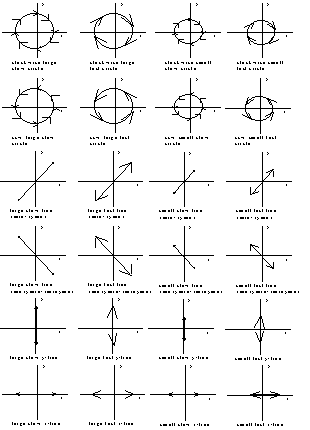
The oscillating circles and lines used in the crane and runway lexicons form the basis of the gestures used in our system. When the geometric features of size and direction are added, the lexicon is expanded to encompass 24 gestures (Figure 2).
Identification Method for Gestures Represented as a Dynamic System
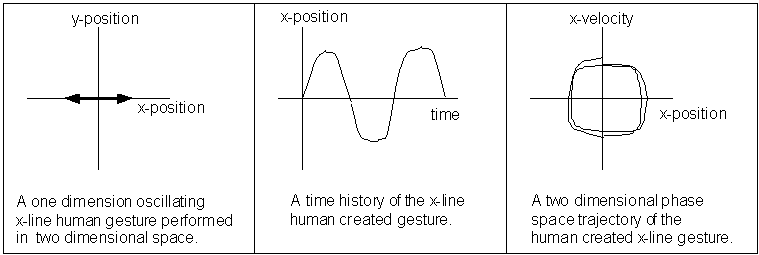
A representative planar gesture, used throughout this section to exemplify our method, consists of a family of oscillating motions which form a (roughly) horizontal line segment ("x-line motion"). Humans are incapable of reliably generating a perfect sinusoidal motion, as we suggest by the illustrated x-line motion shown Figure 3. We find it most convenient to represent such motions as they evolve over time in the x-velocity plotted against the x-position "phase plane" space. This figure, in its evident departure from a pure sinusoid, suggests the natural range of variation that we would nevertheless like to associate with the same gesture. We desire a computationally effective mathematical representation for such gestures.
Out of the enormous variety of possible representations, we choose to rely on the dynamic properties of simple physical motions. A dynamic system is a mathematical model describing the evolution of all possible states in some state space as a function of time [5]. Given an initial state, the evolution over time of subsequent states is called a "trajectory" or "motion". We use a differential equation representation of a dynamic system. Specifically, a vector field, f, parameterized by a carefully chosen combination of tunable constants, q, comprises our representation of gestures and the motions associated with them.
Notation and Terminology.
For ease of exposition, we present in this section the abbreviations
and definitions used throughout this paper. Parameterized differential
equation models can be divided into two types: non-linear-in-parameters
(NLIP) and linear-in-parameters (LIP) (which include linear systems).
The two models can be further subdivided into linear-in-state
(LIS) and non-linear-in-state (NLIS). Given such a representation,
the instantaneous output of our model takes the form of a tangent
vector, 
, that depends upon the present state (input, 
) and parameter setting, q.
Representing Oscillatory Motions.
We "invent" certain differential equations, composed of state variables and parameters, which intuition suggests may represent human gestures. It is advantageous to use a NLIP/NLIS model because it covers a much broader range of systems than an LIP model. However, for reasons to be discussed below, we find it expedient to use a LIP model. We choose to represent planar oscillatory gestures as second order systems with the intuition that a model based on the acceleration (physical dynamics) of a system is sufficient to characterize the gestures in which we are interested.
An LIP representation has the form:
 |
(1) |
where q represents tunable parameters. Fixing the parameters yields a unique set of motions, with different initial conditions. With the intuition in mind of capturing the variability of human motion, each such set of motions we take to represent one specific gesture. Choosing different values of q in a given representation results in a family of sets of motions — a "gesture family".
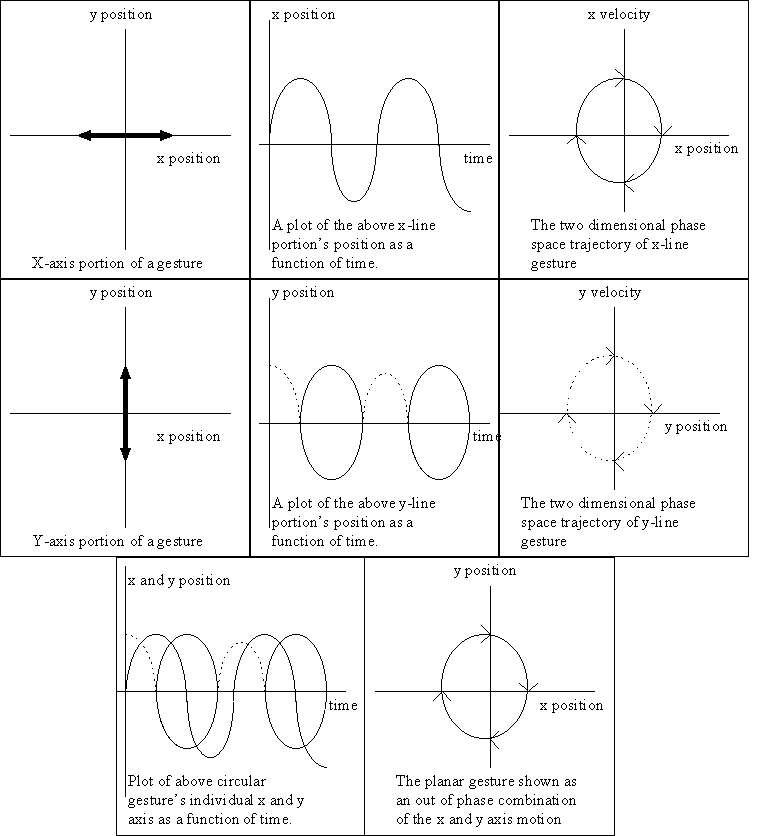
For example, we might represent an oscillatory circular gesture as combinations of two (x and y axis) two-dimensional state space representations:
 |
(2) |
where 
and 
represent the position of
the gesture on the x and y-axis, 
and 
are
its x and y-axis velocity, and 
and 
are
specified parameters. For any constant 
, all
trajectories (on each axis) satisfy 
, as can be seen
by direct differentiation (figure 4). A gesture begun at any point
(initial condition) in its trajectory should still be identified
as the same oscillating line.
Our family of gestures (the family of sets of trajectories) is a mathematical model which contains a finite number of tunable parameters (although, in the final implementation, parameters will not be the sole basis of gesture classification). In order to categorize a finite number of gestures in this family and to permit further variability in the exact motions associated with a particular gesture within this family, we partition the parameter space into a finite number of cells — the "lexicon" — and associate all parameter values in the same cell with one gesture. We use off-line simulations to determine the location of these cells.
Tuning Gesture Model Parameters.
Our gesture model and parameter determination scheme arises from the following considerations. First, we abandon off-line "batch" techniques in favor of on-line "sequential" ones because we desire our recognition system to identify gestures as they are generated.
Previously, in an attempt to use only position data, we considered the possible role of an adaptive estimator (which estimates unknown states for purely LIP/LIS systems). We abandoned this approach because we found the limitation to LIS models could not adequately handle imperfect human gestures.
A Linear Least Squares method (LLS), which makes use of all the data independent of ordering, is our choice for parameter identification. The recursive LLS technique works for LIP, but not NLIP, models.
Given an LIP nth order system (eq. 1), the identification error due to q for all sampled times from 0 to t is:
 |
(3) |
Because the system is LIP, we can uniquely
(assuming a good data set) determine 
based on all input
and output data by a formula which minimizes the above error function.
However, an equivalent sequential version of this batch approach
can be derived by considering each successive error, 
as
the data arrives. Taking the gradient of and
using appropriate algebra yields the sequential update law [7]:
 |
(4) |
where q denotes the present parameter
estimate, and 
denotes the local expression of the batch LLS pseudo-inverse.
Various Gesture Models
The following five LIP models are candidates for circle and
line gesture representations. Each model represents only one dimension
of motion. An oscillating circle or line is formed when two of
these decoupled models are present, one for each planar motion
dimension. The position and velocity states are denoted 
and 
respectfully. They are of
the form 
, and for
| Linear with offset: |
 |
| Van der Pol: |
 |
| Van der Pol with offset: |
 |
| Higher Order Terms: |
 |
| Velocity Damping: |
 |
To use the models described here on a digital computer, a fourth-order Runge-Kutta integration method is used. Simulations showed that a sampling rate of 60 Hz is sufficiently small to allow the use of this method.
Choosing a Gesture Model via Residual Calculation.
A predictor bin, composed of a model with parameters tuned
to represent a specific gesture, determines a gesture's future
position and velocity based on its current state. To measure the
accuracy of the bin's prediction, we compute an instantaneous
residual error, which is the normalized difference between the
bin's prediction and the next gesture state (normalized version
of 
in equation 3). The total residual error is an
exponentially decayed summation of the residual error. A bin that
predicts the future state of a gesture it truly represents should
have a smaller residual error than a bin tuned to other gestures.
For the residual error calculations, we used position and velocity data from slow, medium and fast circular gestures. In simulations, the total residual error was calculated by subjecting each predictor bin to each gesture type. For example, Table 1 lists the residual errors for one of the proposed models.
A measure of a model's usefulness is determined by examining the ratio of the lowest residual error to the next lowest residual error in each column. The worst "residual error ratio" is the smallest ratio from all the columns because it is easier to classify a gesture when the ratio is large. A comparison of the worst "residual error ratio" of each model we consider is summarized in Figure 5, and suggests that the velocity damping model is the best choice for our application. However, for our on-line gesture recognition experiments, we will use the model with the clearest physical meaning, Linear with Offset Component, so we can both most intuitively assess our results and determine if gesture discrimination is possible when the residual ratio is that large.
|
|
||||||
| slow | medium | fast | ||||
| slow bin | 1.31 | 1.20 | 1.37 | |||
| medium bin | 14.1 | 0.24 | 1.01 | |||
| fast bin | 424 | 23.1 | 0.23 | |||
Table 1: Residual Errors of Linear with Offset Cmponent Model
A Dynamic Gesture Recognition and Control System
In this section we detail the specific components of the dynamic gesture recognition system. Figure 6 illustrates the signal flow from gesture creation, sensing, identification, and transformation into an executed robot response. The gesture recognition system is implemented on a INMOS based distributed transputer control system built by Rizzi et. al .[9], that also inspired this architecture.
System Modules.
In module G, the Gesture Creator, a human moving a flashlight against a black background creates a gesture. Our gesture lexicon, the set of gestures our system can recognize, consists of 24 planar oscillators. The user signals the start and stop of a gesture by turning the flashlight on and off, thus enabling isolation of gestures, one from another. The sensor module detects the light from the flashlight.
Figure 6: Model residual ratios: the Velocity Damping model discriminates most effectively, and the Van der Pol model discriminates least effectively, for the data considered
The Sensor Module, S, using the Cyclops vision system [9], detects the gesture by transforming the light from a flashlight bulb into x and y position and velocity coordinates, sending them to the Predictor Module at a rate of 60 Hz.
The Predictor Module, P, contains a bank of predictor bins (inspired by Narendra and Balakrishnan's work [8]), as shown in Figure 7. Each predictor bin contains a dynamic system model with parameters preset to a specific gesture. We assume that the motions of human circular gestures are decoupled in x and y. Therefore, there are separate predictor bins for the x and y axes. Since there are three basic gestures, a total of six predictor bins is required.
Each bin's model is used to predict the future position and velocity of the motion by feeding the current state of the motion into the gesture model and computing a residual error. The bin, for each axis, with the least residual error is the best gesture match. If this lowest value is not below a predefined threshold, then the result is ignored; no gesture is identified. Otherwise, geometric information is used to constrain the gesture further. A single gesture identification number, which represents the combination of the best x bin, the best y bin, and the geometric information, is outputted to the transformation module upon the initiation of the gesture, and is continually updated until the flashlight turns off.
The predictor module also contains two bins, one for each axis, for identifying the actual parameters of human generated motions using the linear least squares technique. During our research, these "gesture parameter identification bins" were used to recompute the parameters seeded in each predictor bin and to allow users to confirm that they presented the gestures they intended. The states of the identification bins are reset at the beginning of each new gesture.
The Transformation module, T, uses the gesture classification to determine an appropriate response for the controlled robot. The response in this system is a reference trajectory which, when followed by a camera neck, will "mimic" the observed gesture. This allows the person creating the gesture to know immediately if the recognition system properly identified the gesture.
The actuated mechanism, module R, tracks the reference trajectory using an inverse dynamics controller.
Experiments and Results
Two types of experiments were performed. The first experiment, trial "A", was designed to test the gesture recognition system's ability to recognize gestures despite the fact that humans vary the way they make the same gesture. In this experiment, the subject repeated each gesture in the lexicon twenty times. In the second experiment type, trials "B", "C", and "D", we tested how well the system can recognize gestures when presented with different gestures in a random order by having subjects perform gestures from a randomly ordered list: "B" contained "large gestures", "C" contained "circular gestures", and "D" contained all types.
The experimental results are summarized in Table 2, showing that the system achieves a greater than 85% correct classification rate. Note that two subjects performed all experiments, while two others performed only "B" and "C".
| Subject | A | B | C | D |
| 0 | 87% | 92% | 94% | 90% |
| 1 | 91% | 86% | 86% | 86% |
| 2 | n/a | 86% | 90% | n/a |
| 3 | n/a | 90% | 90% | n/a |
Table 2: Recognition Experiment Results.
System Features.
As a natural byproduct of the gesture’s dynamic systems representation, our system requires a small amount of memory because it stores a representation of the gesture "generator" (Equation 1), rather than of the spatial array of data (Figure 3). Specifically, the memory required increases linearly with the size of the gesture lexicon and with the number of model parameters.
The use of a predictor results in small computational requirements for gesture recognition. These computations can be performed at camera field rate (60 Hz) (other experiments have shown that the prediction module still functions at field rate at least up to a ten parameter model). Additional small memory parallel processors could be added to allow for an increased lexicon, with the calculations farmed out to the added processors.
Extensions
We can extend our gesture recognition by expanding the types of planar oscillators it can recognize, using it to control a more complicated robot platform, and by using it for the remote control of devices.
Non-linear Gestures
Human gestures consist of more than basic circles and lines. The "come here" or "go there" motions represent a useful class of gestures that our system should be able to identify. A person creates a "come here" motion by sweeping one hand repeatedly, first quickly toward their body then slowly away. A non-linear-in-state model is required to represent these types of gestures due to the dynamics of their motions. Therefore, we define these motions as non-linear gestures, and used a variation of the velocity damping model to represent them [2].
Gestural Mobile Robot Control
Our gestural control system could be mapped to control a wheeled mobile robot with an attached camera. To design a viable device, we would match specific gestures to appropriate system responses. Circular oscillator gestures would control the on-board camera's pan and tilt motion, while non-linear and line oscillator gestures would control the robot's path.
Gestural Control of Devices in a Two-Way Visual Communications Environment.
These gestures could also be used in special two-way video communication environments [4]. Figure 8 depicts the two-way video feedback control architecture. A camera-based control view is sent from a remote location to a local control site. A video icon replaces the flashlight as the tracked feature making a gesture. This moving icon is superimposed on the control view of the remote environment, and the newly combined video stream is sent back to the remote site. The icon is extracted from the video stream at the remote site and, when a predictor module is installed, used to create a control command.
Acknowledgment
We thank Dr. Al Rizzi for his advice concerning various technical and theoretical aspects of this work.
Bibliography
[1] R. L. Birdwhistell. Kinesics and Context; essays on body motion communication. Phila., PA, 1970.
[2] C. Cohen. Dynamical system representation, generation, and recognition of basic oscillatory motion gestures and applications for the control of actuated mechanisms. Ph.D. Dissertation, U. of Mich., 1996.
[3] Link-Belt Construction Equipment Company. Operating safety: Cranes and excavators, 1987.
[4] L. Conway. System and method for teleinteraction. U.S. Patent 5,444,476, August 1995.
[5] M. Hirsch and S. Smale. Differential Equations, Dynamical Systems, and Linear Algebra. Academic Press, Inc., Orlando, Florida, 1974.
[6] E. Klima and U. Bellugi. Language in another mode. Language and brain: Developmental aspects, Neurosciences research prog. bulletin., 12(4):539-550, 1974.
[7] P. Kumar and P. Varaiya. Stochastic Systems: Estimation, Identification, and Adaptive Control. Prentice-Hall, Inc., Englewood Cliffs, NJ, 1986.
[8] K. Narendra and J. Balakrishnan. Improving transient response of adaptive control systems using multiple models and switching. IEEE Trans. On Auto. Control, 39:1861-1866, Sept 1994.
[9] A. Rizzi, L. Whitcomb, and D. Koditschek. Distributed real-time control of a spatial robot juggler. IEEE Computer, 25(5), May 1992.
[10] FAA U.S. Dept. of Transportation. Aeronautical information manual: official guide to basic flight information and ATC procedures, 1995.